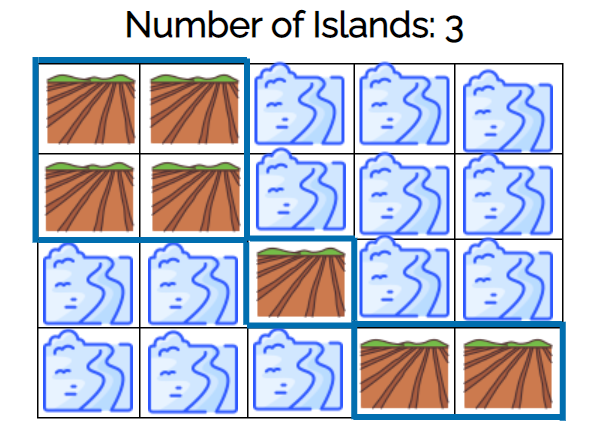
Number of Islands

Level - Medium

Statement:

Given an m x n 2D binary grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Example 2

Input: grid = [
  ["1","1"],
  ["1","0"],
  ["1","0"],
  ["0","0"]
]
Output: 1

You can try this at:

• https://leetcode.com/problems/number-of-islands/

Algorithm

1. Initialize a queue<int[]> to store the co-ordinates(x,y) of the elements in the grid and a visited array to keep track of the visited elements.
2. Loop through all the elements in the grid.
3. If the element is 1(land) and has not been visited before, increment the count of islands and perform BFS on that element.
4. To perform BFS on an element:
   • Initialize the queue with the starting co-ordinate(0,0) and mark it as visited by setting visited[x][y] = true.
   • Loop through the following steps until the queue is empty:
     • Poll the co-ordinate from the queue.
     • Move in all four directions (up, down, left, and right) and if an element in any direction is 1 and has not been visited, put that co-ordinate in the queue and mark it as visited.
   • After the BFS is complete, we will have visited all the elements in the island. We will continue to loop through the grid and perform BFS on any unvisited 1(land) elements until we have found all the islands.
5. Return the count of islands

Code

Java

 public void bfs(int x,int y,char[][] grid,boolean[][] visited,int n,int m){
        Queue<int[]> q = new LinkedList<>();
        int[] dx = {0,0,-1,1};
        int[] dy = {-1,1,0,0};

        // init the queue
        q.add(new int[]{x,y});visited[x][y] = true;
        while(!q.isEmpty()){
            int[] point = q.poll();
            // go to all the directions
            for(int i=0;i<4;i++){
                int new_x = dx[i]+point[0],new_y = dy[i]+point[1];
                if(new_x>=0 && new_x<n && new_y>=0 && new_y<m && grid[new_x][new_y]=='1' && !visited[new_x][new_y]){
                    q.add(new int[]{new_x,new_y});
                    visited[new_x][new_y] = true;
                }
            }
        }
        return;
    }
    public int numIslands(char[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        // track visited to avoid infinite loop
        boolean[][] visited = new boolean[n][m];
        int count = 0;

        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(grid[i][j]=='1' && !visited[i][j]){
                    count++;
                    bfs(i,j,grid,visited,n,m);
                }
            }
        }

        return count;
    }

Python

from collections import deque

class Solution:
    def bfs(self, x, y, grid, visited, n, m):
        queue = deque()
        dx = [0, 0, -1, 1]
        dy = [-1, 1, 0, 0]

        # Initialize the queue
        queue.append((x, y))
        visited[x][y] = True

        while queue:
            point = queue.popleft()

            # Go to all directions
            for i in range(4):
                new_x = dx[i] + point[0]
                new_y = dy[i] + point[1]

                if (
                    0 <= new_x < n
                    and 0 <= new_y < m
                    and grid[new_x][new_y] == '1'
                    and not visited[new_x][new_y]
                ):
                    queue.append((new_x, new_y))
                    visited[new_x][new_y] = True

    def numIslands(self, grid):
        n = len(grid)
        m = len(grid[0])

        # Track visited to avoid infinite loop
        visited = [[False] * m for _ in range(n)]
        count = 0

        for i in range(n):
            for j in range(m):
                if grid[i][j] == '1' and not visited[i][j]:
                    count += 1
                    self.bfs(i, j, grid, visited, n, m)

        return count

CPP

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Solution {
public:
    void bfs(int x, int y, vector<vector<char>>& grid, vector<vector<bool>>& visited, int n, int m) {
        queue<pair<int, int>> q;
        vector<int> dx = {0, 0, -1, 1};
        vector<int> dy = {-1, 1, 0, 0};

        // Initialize the queue
        q.push(make_pair(x, y));
        visited[x][y] = true;

        while (!q.empty()) {
            pair<int, int> point = q.front();
            q.pop();

            // Go to all directions
            for (int i = 0; i < 4; i++) {
                int new_x = dx[i] + point.first;
                int new_y = dy[i] + point.second;

                if (new_x >= 0 && new_x < n && new_y >= 0 && new_y < m && grid[new_x][new_y] == '1' && !visited[new_x][new_y]) {
                    q.push(make_pair(new_x, new_y));
                    visited[new_x][new_y] = true;
                }
            }
        }
    }

    int numIslands(vector<vector<char>>& grid) {
        int n = grid.size();
        int m = grid[0].size();

        // Track visited to avoid infinite loop
        vector<vector<bool>> visited(n, vector<bool>(m, false));
        int count = 0;

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    count++;
                    bfs(i, j, grid, visited, n, m);
                }
            }
        }

        return count;
    }
};

Complexity

Time Complexity:

O(N*N))

Space Complexity:

O(N*N)