Introduction for BFS(Breath First Search)

What is BFS ?

BFS stands for Breadth First Search, it is an algorithm which helps us to traverse the Graph. so BFS algorithms are generally used in solving graph related problems.

We put BFS section inside Queue because it uses Queue as a data structure to traverse in desired manner.

Example

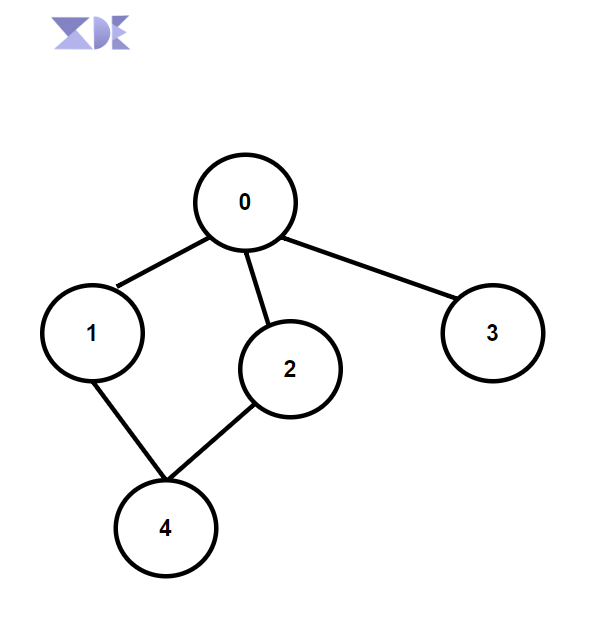
Lets take undirected graph for illustration

Graph Representation

Node 0 -> Node 1 , Node 2 , Node 3
Node 1 -> Node 0 , Node 4
Node 2 -> Node 0 , Node 4
Node 3 -> Node 0
Node 4 -> Node 1 , Node 2

adjacency_list: [[1,2,3],[0,4],[0,4],[0],[1,2]] 
V(number of vertices): 5

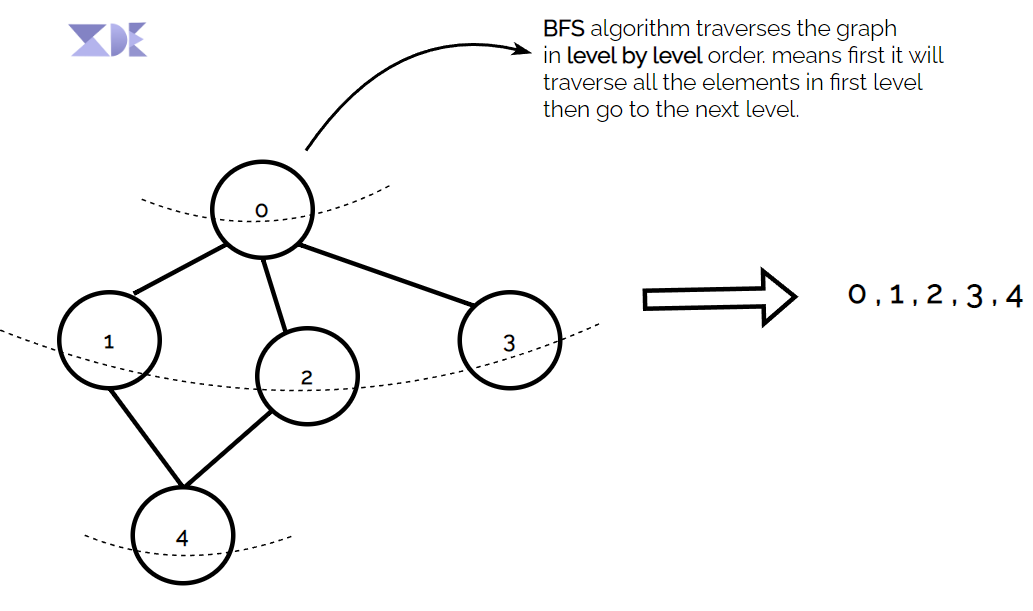
BFS Traversal Manner

BFS Algorithmic Walkthrough

The working of BFS algorithm can be described as follows:

• Initialize the algorithm with a starting vertex (or node) and mark it as visited.
• Add the starting vertex to a queue.
• While the queue is not empty, do the following:
  • Remove the first vertex from the queue and print it.
  • For each neighbor of the vertex, if it is not visited, mark it as visited and add it to the queue.
• Repeat step 3 until the queue becomes empty.

In other words, BFS explores the graph in a level-by-level manner, visiting all the nodes at a particular distance from the starting node before moving on to the next level. This ensures that the algorithm visits all the nodes in the graph in the shortest possible path.

Intution behind BFS Algorithm

Code

Java

import java.util.*;

class Main {
    public static void main(String[] args) {
        int[][] adj_list = {{1,2,3},{0,4},{0,4},{0},{1,2}};
        int V = 5; 
        int[] res = bfs(adj_list,V);
        for(int r: res)System.out.print(r+" ");
    }
    public static int[] bfs(int[][] adj_list,int V){
        int[] res = new int[V];
        Queue<Integer> q = new LinkedList<>(); 
        // visited array to avoid the loop
        boolean[] vis = new boolean[V];
        //init the queue and visit the source
        q.add(0);vis[0] = true;
        int index = 0;
        //iterate the queue
        while(!q.isEmpty()){
            int peak = q.poll();
            // add it to the result
            res[index++] = peak;
            
            // iterate through all the neighbours
            for(int neigh: adj_list[peak]){
                // not visited neighbours
                if(!vis[neigh]){
                    // add in queue and visit the node 
                    q.add(neigh);
                    vis[neigh] = true;
                }
            }
        }
        return res;
    }
}    

Python

import queue

def bfs(adj_list, V):
    res = [0] * V
    q = queue.Queue()
    vis = [False] * V

    q.put(0)
    vis[0] = True
    index = 0

    while not q.empty():
        peak = q.get()
        res[index] = peak
        index += 1

        for neigh in adj_list[peak]:
            if not vis[neigh]:
                q.put(neigh)
                vis[neigh] = True

    return res

adj_list = [[1, 2, 3], [0, 4], [0, 4], [0], [1, 2]]
V = 5
res = bfs(adj_list, V)
print(res)

CPP

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> bfs(vector<vector<int>>& adj_list, int V) {
    vector<int> res(V);
    queue<int> q;
    vector<bool> vis(V, false);

    q.push(0);
    vis[0] = true;
    int index = 0;

    while (!q.empty()) {
        int peak = q.front();
        q.pop();
        res[index++] = peak;

        for (int neigh : adj_list[peak]) {
            if (!vis[neigh]) {
                q.push(neigh);
                vis[neigh] = true;
            }
        }
    }

    return res;
}

int main() {
    vector<vector<int>> adj_list = {{1, 2, 3}, {0, 4}, {0, 4}, {0}, {1, 2}};
    int V = 5;
    vector<int> res = bfs(adj_list, V);
    
    for (int r : res) {
        cout << r << " ";
    }

    return 0;
}

Complexity

Time Complexity:

O(V+E)

Space Complexity:

O(V)

note

V denotes Vertex/Nodes and E denotes Edges in a Graph.