Introduction to Flood Fill Algorithm

Level - Easy

Statement

An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.You are also given three integers sr, sc, and color. Perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on.

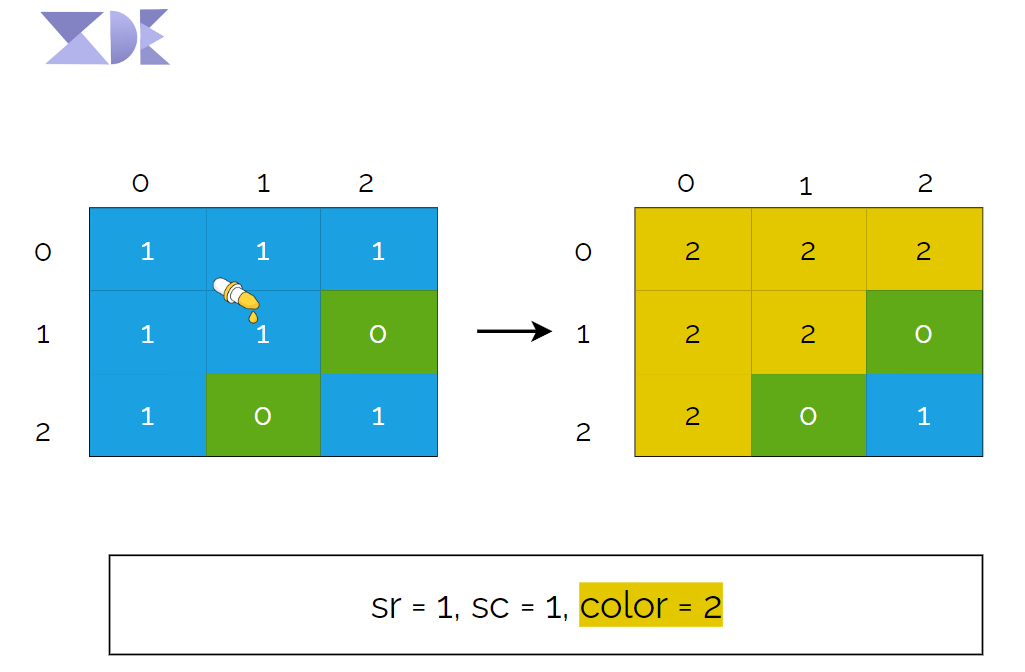
Example

Input:

image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2

Output:

[[2,2,2],[2,2,0],[2,0,1]

You can try this at:

• https://leetcode.com/problems/flood-fill/

Algorithm Steps

1. Start with the initial position (sr, sc) in the image and the desired color to fill.
2. Retrieve the old_color at the starting position (sr, sc) from the image.
3. If the old_color is already equal to the desired color, no further action is required. Return the image as it is.
4. Call the dfs function to perform a depth-first search starting from the initial position (sr, sc).
5. In the dfs function:
   • Check if the current position (sr, sc) is out of bounds (less than 0 or greater than or equal to the size of the image), and if so, return (base case).
   • Check if the color at the current position (sr, sc) is equal to the old_color, and if not, return (base case).
   • Change the color at the current position (sr, sc) to the desired new_color.
   • Recursively call the dfs function for the four adjacent positions by adding the corresponding values from dx and dy arrays to sr and sc, respectively.
6. Once the dfs function completes, return the modified image.
7. The algorithm will fill the connected region in the image starting from the initial position (sr, sc) with the desired color.
8. Any other disconnected regions with the same color will remain unchanged.

Algorithm Dry Run(Visual Walkthrough)

Implementation

Java

class Solution {
    int[] dx = {-1,1,0,0};
    int[] dy = {0,0,-1,1}; 
    public void dfs(int[][] image, int sr, int sc, int new_color,int old_color){
        if(sr < 0 || sc < 0 || sr >= image.length || sc >= image[0].length)return;// base case
        if(image[sr][sc]!=old_color)return;// base case don't change color if it is diff than old_color
        
        image[sr][sc] = new_color;// change the color

        // try all 4 directions
        for(int i=0;i<4;i++){
            int new_x = dx[i] + sr;
            int new_y = dy[i] + sc;
            dfs(image,new_x,new_y,new_color,old_color);
        }
    }
    public int[][] floodFill(int[][] image, int sr, int sc, int color) {
        int old_color = image[sr][sc];
        if(old_color!=color)dfs(image,sr,sc,color,old_color);
        return image;
    }
}

CPP

class Solution {
private:
    vector<int> dx = {-1, 1, 0, 0};
    vector<int> dy = {0, 0, -1, 1};
    
    void dfs(vector<vector<int>>& image, int sr, int sc, int new_color, int old_color) {
        if (sr < 0 || sc < 0 || sr >= image.size() || sc >= image[0].size())
            return;  // base case
        if (image[sr][sc] != old_color)
            return;  // base case, don't change color if it is different than old_color

        image[sr][sc] = new_color;  // change the color

        // try all 4 directions
        for (int i = 0; i < 4; i++) {
            int new_x = dx[i] + sr;
            int new_y = dy[i] + sc;
            dfs(image, new_x, new_y, new_color, old_color);
        }
    }

public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        int old_color = image[sr][sc];
        if (old_color != color)
            dfs(image, sr, sc, color, old_color);
        return image;
    }
};

Python

class Solution:
    dx = [-1, 1, 0, 0]
    dy = [0, 0, -1, 1]
    
    def dfs(self, image, sr, sc, new_color, old_color):
        if sr < 0 or sc < 0 or sr >= len(image) or sc >= len(image[0]):
            return  # base case
        if image[sr][sc] != old_color:
            return  # base case, don't change color if it is different than old_color

        image[sr][sc] = new_color  # change the color

        # try all 4 directions
        for i in range(4):
            new_x = self.dx[i] + sr
            new_y = self.dy[i] + sc
            self.dfs(image, new_x, new_y, new_color, old_color)
    
    def floodFill(self, image, sr, sc, color):
        old_color = image[sr][sc]
        if old_color != color:
            self.dfs(image, sr, sc, color, old_color)
        return image

Complexity

Time Complexity:

O(M*N)

Space Complexity:

O(M*N)