Introduction of Dijkstra's algorithm

What is Dijkstra's algorithm ?

Dijkstra's algorithm is an algorithm for finding the shortest path from source node to all other nodes in a weighted graph. that's why we called this algorithm as a Single Source Shortest Path.

note

weights should be non-negative otherwise it will create a negative weight cycle which in turns produce the infinite loop

Example

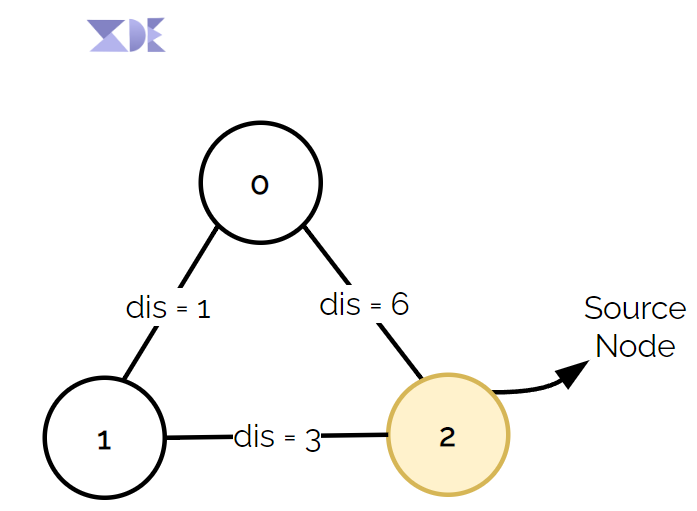
Lets take a weighted and undirected graph for illustration

Graph Representation

Input:

V(Vertex) = 3 , E(Edges) = 3 , S(Source) = 2
edges[][] = [ [0,1,1] , [1,2,3] , [0,2,6] ]

Output:

dis[]  -> [4 , 3 , 0]
index  -> [0 , 1 , 2]

edges[i] = [u,v,w], where u and v are nodes and w is distance between u and v.

dis[i] = distance between node i and source node

Convert input edges into adjacency list

generally in problem solving questions related to graph we are provided the edges in the input, but that's not the actual representation of graph.

actual representation of graph is adjacency list or adjacency matrix.

hence we need to convert input edges into adjacency list.

Working of Algorithm

1. mark the distance to each node as infinity, except for the source node, which is marked as 0.
2. Start from the source node and mark it as current node and enter it into min heap priority queue.
3. pull the node from min heap priority queue
   • calculate the distance to that neighbor using distance upto current node + distance from current to neighbor node
   • If this distance is less than the neighbor's current distance, update the neighbor's distance and put it into min heap priority queue.
4. repeat step 3 until we have node in min heap priority queue

Intution of Algorithm

We use a min heap priority queue because it allows us to efficiently access the vertex with the smallest distance from the source vertex.

In the context of Dijkstra's algorithm, we can store each vertex in the min heap priority queue along with its current distance from the source vertex.

By maintaining this min heap property, we ensure that the vertex with the smallest distance is always at the top of the heap, so we can easily access and explore the next vertex with the smallest distance.

You can try this at:

• https://practice.geeksforgeeks.org/problems/implementing-dijkstra-set-1-adjacency-matrix/1

Code

Java

import java.util.*;

class Main{
    // main function
    public static int[] dijkstra(int V, ArrayList<ArrayList<int[]>> adj, int S)
    {
        int[] dis = new int[V];// distance array
        // distance from source to all other nodes is infinite for now except source node
        for(int i=0;i<V;i++){
            if(S!=i)dis[i] = Integer.MAX_VALUE;
        }
        // Priority Queue to select the shortest distance first, min-heap priority queue
        PriorityQueue<Node> pq = new PriorityQueue<>((a,b)->a.dis-b.dis);
        pq.add(new Node(S,0));// add source node to S and dis to be 0 
        while(!pq.isEmpty()){
            Node element = pq.poll();// poll the node
            int node = element.node,wt = element.dis;
            // get all the neighbour of node
            ArrayList<int[]> neighbours = adj.get(node);
            for (int[] neigh : neighbours) {
                int neigh_node = neigh[0] , dis_from_node = neigh[1];
                // if we have a path to get minimum distance
                if(wt+dis_from_node < dis[neigh_node]){
                    dis[neigh_node] = wt+dis_from_node;
                    pq.add(new Node(neigh_node,dis[neigh_node]));
                }
            }
        }
        return dis;
    }
    public static ArrayList<ArrayList<int[]>> createGraph(int V,int E,int[][] edges){
        ArrayList<ArrayList<int[]>> adj = new ArrayList<>();
        // there are V nodes
        for(int i=0;i<V;i++){
            adj.add(new ArrayList<>());
        }
        // iterate through all the edges
        for(int i=0;i<E;i++){
            int[] edge = edges[i];
            int u = edge[0],v = edge[1],w = edge[2];
            adj.get(u).add(new int[]{v,w});// connect u to v with weight w
            adj.get(v).add(new int[]{u,w});// connect v to u with weight w
        }
        return adj;
    }
    public static void main(String args[]){
        // input section
        int V = 3,E = 3,S = 2;// V is number of nodes and E is number of edges, S is source node
        int[][] edges = {{0,1,1},{1,2,3},{0,2,6}};// each array consists of {u,v,w}
        ArrayList<ArrayList<int[]>> adj = createGraph(V,E,edges);  
        int[] res = dijkstra(V, adj, S);
        // print output
        for(int r: res)System.out.print(r+" ");
    } 
}

class Node{
  int node, dis;
  Node(int _node,int _dis){
    this.node = _node;
    this.dis = _dis;
  }
}

Python

import heapq

class Node:
    def __init__(self, node, dis):
        self.node = node
        self.dis = dis
    
    def __lt__(self, other):
        return self.dis < other.dis

def dijkstra(V, adj, S):
    dis = [float('inf')] * V  # distance array
    dis[S] = 0  # distance from source to itself is 0
    pq = []  # Priority Queue to select the shortest distance first
    heapq.heappush(pq, Node(S, 0))  # add source node to S and dis to be 0
    while pq:
        element = heapq.heappop(pq)  # pop the node
        node, wt = element.node, element.dis
        # get all the neighbors of node
        neighbors = adj[node]
        for neigh in neighbors:
            neigh_node, dis_from_node = neigh[0], neigh[1]
            # if we have a path to get a minimum distance
            if wt + dis_from_node < dis[neigh_node]:
                dis[neigh_node] = wt + dis_from_node
                heapq.heappush(pq, Node(neigh_node, dis[neigh_node]))
    return dis

def createGraph(V, E, edges):
    adj = [[] for _ in range(V)]  # create adjacency list
    for edge in edges:
        u, v, w = edge
        adj[u].append([v, w])  # connect u to v with weight w
        adj[v].append([u, w])  # connect v to u with weight w
    return adj

# input section
V, E, S = 3, 3, 2  # V is number of nodes, E is number of edges, S is source node
edges = [[0, 1, 1], [1, 2, 3], [0, 2, 6]]  # each array consists of [u, v, w]
adj = createGraph(V, E, edges)
res = dijkstra(V, adj, S)
# print output
print(res)

CPP

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <functional>
using namespace std;

struct Node {
    int node, dis;
    Node(int _node, int _dis) : node(_node), dis(_dis) {}
};

vector<int> dijkstra(int V, vector<vector<pair<int, int>>>& adj, int S) {
    vector<int> dis(V, INT_MAX);  // distance array
    dis[S] = 0;  // distance from source to itself is 0
    priority_queue<Node, vector<Node>, function<bool(Node, Node)>> pq([](Node a, Node b) { return a.dis > b.dis; });  // min-heap priority queue
    pq.push(Node(S, 0));  // add source node to S and dis to be 0
    while (!pq.empty()) {
        Node element = pq.top();  // get the node with the minimum distance
        pq.pop();
        int node = element.node, wt = element.dis;
        // get all the neighbors of node
        vector<pair<int, int>>& neighbors = adj[node];
        for (pair<int, int>& neigh : neighbors) {
            int neigh_node = neigh.first, dis_from_node = neigh.second;
            // if we have a path to get a minimum distance
            if (wt + dis_from_node < dis[neigh_node]) {
                dis[neigh_node] = wt + dis_from_node;
                pq.push(Node(neigh_node, dis[neigh_node]));
            }
        }
    }
    return dis;
}

vector<vector<pair<int, int>>> createGraph(int V, int E, vector<vector<int>>& edges) {
    vector<vector<pair<int, int>>> adj(V);  // create adjacency list
    for (vector<int>& edge : edges) {
        int u = edge[0], v = edge[1], w = edge[2];
        adj[u].push_back({ v, w });  // connect u to v with weight w
        adj[v].push_back({ u, w });  // connect v to u with weight w
    }
    return adj;
}

int main() {
    // input section
    int V = 3, E = 3, S = 2;  // V is number of nodes, E is number of edges, S is source node
    vector<vector<int>> edges = { {0, 1, 1}, {1, 2, 3}, {0, 2, 6} };  // each array consists of {u, v, w}
    vector<vector<pair<int, int>>> adj = createGraph(V, E, edges);
    vector<int> res = dijkstra(V, adj, S);
    // print output
    for (int r : res) {
        cout << r << " ";
    }
    cout << endl;
    return 0;
}

Complexity

Time Complexity:

O(Vlog(V) + E)

Space Complexity:

O(V + E)

note

V denotes number of Vertex/Nodes and E denotes number of Edges in a Graph.

Problem Solving Questions

• network delay time